PROPORCIONALIDAD

1. PROPORCIONALIDAD

Dos magnitudes son directamente proporcionales si al multiplicar o dividir una de ellas por un número, la otra queda multiplicada o dividida por ese mismo número. Al dividir cualquier valor de la segunda magnitud por su correspondiente valor de la primera magnitud, se obtiene siempre el mismo valor (constante).Al dividir cualquier valor de la segunda magnitud por su correspondiente valor de la primera magnitud, se obtiene siempre el mismo valor (constante). A esta constante se le llama razón de proporcionalidad directa.

Para resolver un ejercicio de proporcionalidad directa se puede utilizar:

• La razón de proporcionalidad.
• Una regla de tres.
• El método de reducción a la unidad.

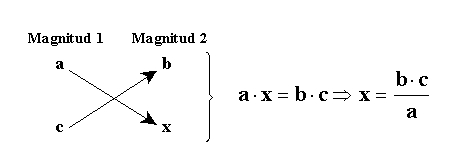Problemas de proporcionalidad

Al llegar al hotel nos han dado un mapa con los lugares de interés de la ciudad, y nos dijeron que 5 centímetros del mapa representaban 600 metros de la realidad. Hoy queremos ir a un parque que se encuentra a 8 centímetros del hotel en el mapa. ¿A qué distancia del hotel se encuentra este parque?

Para resolver este problema, debemos pensar en primer lugar si cumple una proporcionalidad directa o inversa. Para ello, pensamos…

Si en lugar de 5 centímetros hablásemos del doble de centímetros en el mapa (10 centímetros), ¿en la realidad serían más metros o menos metros?

Serían más metros: justo el doble de metros en la realidad.

Si al duplicar una magnitud (centímetros) también se duplica la otra (metros) estamos hablando de una proporcionalidad directa

Por lo tanto, vamos a resolver el problema:

Como 5 centímetros representan 600 metros, 1 centímetro representará

600 : 5 = 120 metros

120 x 8 = 960 metros

Solución: El parque se encuentra a 960 metros del hotel.

segunda problema de proporcionalidad.

Ayer 2 camiones transportaron una mercancía desde el puerto hasta el almacén. Hoy 3 camiones, iguales a los de ayer, tendrán que hacer 6 viajes para transportar la misma cantidad de mercancía del almacén al centro comercial. ¿Cuántos viajes tuvieron que hacer ayer los camiones?

Nos preguntamos si cumple una proporcionalidad directa o inversa. Para ello, pensamos.

i en lugar de 3 camiones hablásemos del doble de camiones (6 camiones), ¿tendrían que hacer más o menos viajes?

 Cuantos más camiones carguen mercancía, en menos viajes se cargará toda: necesitarían justo la mitad de viajes.

Si al duplicar una magnitud (camiones) se divide entre dos la otra (viajes necesarios) estamos hablando de una proporcionalidad inversa.

Por lo tanto, vamos a resolver el problema:

Como 3 camiones necesitan hacer 6 viajes, 1 solo camión necesitaría hacer…

3 x 6 = 18 viajes

Como 1 solo camión necesitaría hacer 18 viajes, los 2 camiones tuvieron que hacer…

18 : 2 = 9 viajes

Solución: Ayer los 2 camiones hicieron 9 viajes cada uno.